.
Boolean Algebra
Boolean Algebra is used to analyze and simplify the digital ( logic) circuits. Boolean algebra sometimes referred to as the algebra of logic, is a two valued system of algebra that represents logical relationships and operations. English logician and mathematician George Boole, the first to apply these algebraic techniques to the logic process, contended that any statement (any declarative sentence that is either true or false but not both) could be assigned a binary value, such as "true/false" or "yes/no" or "on/off" of "0/1".
In 1854, Boole wrote An Investigation of the Laws of Thought, in which he discussed ways of reducing logical relationships to simple statements of equality, inequality, inclusion and exclusion. Boole then showed ways to express these statements symbolically, using binary ( two-valued) code, and created algebraic rules that governed these logical relationships.
Truth Table Function
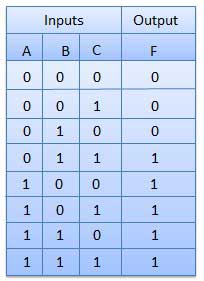
A truth table represents a table having all combinations of inputs and their corresponding result. It is possible to convert the switching equation into a truth table. For example, Consider the following switching equation.
F (A,B,C) = A+BC
The output will be high (1) if A = 1 or BC = 1 or both are 1. The truth table for this equation is shown by Table (a). The number of rows in the truth table is 2nwhere n is the number of input variables (n=3 for the given equation). Hence there are 23 = 8 possible input combination of inputs.
Boolean Function
A Boolean function refers to a function having n number of entries or variables, so it has 2n number of possible combinations of the given variables.
Boolean expressions are formed by application of basic operations to one or more Boolean variable or constants. The simplest expression consists of a single constant or variable such as 0, x or x'. A Boolean expression that contains n distinct variables is usually referred to as a Boolean expression of n variables. Each variable or its complement in an expression is referred as literal.
Boolean expression represents a Boolean function. Substituting 0 and 1 for variable in the expression obtains the value of this function. A truth table specifies the values of a Boolean expression for every possible combination of values of the variables in the expression.
|
A |
B |
B' |
F(A,B) = A + B' |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
Table : Truth table of f(A,B) = A + B'
It is to be noted that different Boolean expression may determine the same Boolean function. Two function. For example A.(B + C) and (A.B) + (A.C) determine the same Boolean function.
Comments
Post a Comment